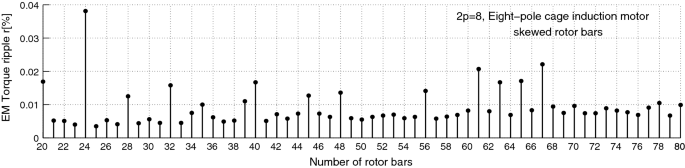
Slot Harmonics Define
In this article we will discuss about: 1. Definition of Harmonics 2. Harmonic Number (h) 3. Types 4. Causes.
- Behind the holes are chambers containing at least one reed. A harmonica reed is a flat elongated spring typically made of brass or bronze, which is secured at one end over a slot that serves as an airway. When the free end is made to vibrate by the player's air, it alternately blocks and unblocks the airway to produce sound.
- Sinusoidal terms (harmonics) whose frequencies are whole multiples of the fundamental frequency, A DC component, where applicable. The nth order harmonic (commonly referred to as simply the nth harmonic) in a signal is the sinusoidal component with a frequency that is n times the fundamental frequency.
The presence of rotor slot harmonics and explains how the stator current is influenced by voltage unbalance. Simulations results have shown excellent match with theoretically predicted harmonic components. K e y w o r d s: induction motor, rotor slot harmonics, voltage unbalance, Fourier series, diagnostics 1 INTRODUCTION.
Definition of Harmonics:
Harmonics are sinusoidal voltages or currents having frequencies that are integer multiples of the frequency at which the supply system is designed to operate.
Harmonics as pure tones making up a composite tone in music. A pure tone is a musical sound of a single frequency, and a combination of many pure tones makes up a composite sound. Sound waves are electromagnetic waves travelling through space as a periodic function of time. Can the principle behind pure music tones apply to other functions or quantities that are time dependent?
ADVERTISEMENTS:
In the early 1800s, French mathematician, Jean Baptiste Fourier formulated that a periodic non-sinusoidal function of a fundamental frequency f may be expressed as the sum of sinusoidal functions of frequencies which are multiples of the fundamental frequency. In our discussions here, we are mainly concerned with periodic functions of voltage and current due to their importance in the field of power quality. In other applications, the periodic function might refer to radiofrequency transmission, heat flow through a medium, vibrations of a mechanical structure, or the motions of a pendulum in a clock.
A sinusoidal voltage or current function that is dependent on time t may be represented by the following expressions:
Voltage function,
v(t) = V sin (ωt) …(4.1)
Current function,
i(t) = I sin (ωt ± θ) …(4.2)
where, ω = 2πf is known as the angular velocity of the periodic waveform and 0 is the difference in phase angle between the voltage and the current waveforms referred to as a common axis. The sign of phase angle θ is positive if the current leads the voltage and negative if the current lags the voltage.
Figure 4.1 contains voltage and current waveforms expressed by Eqs. (4.1) and (4.2) and which by definition are pure sinusoids.
For the periodic non-sinusoidal waveform shown in Fig. 4.2, the simplified Fourier expression states-
V (t) = V0 + V1 sin(ωt) + V2 sin(2 ωt) + V3 sin(3 ωt) + … + Vn sin( n ωt) + Vn+1 sin (( n + 1) ωt) +………….. (4.3)
The Fourier expression is an infinite series. In this equation, V0 represents the constant or the DC component of the waveform.
V1, V2, V3, … , Vn are the peak values of the successive terms of the expression. The terms are known as the harmonics of the periodic waveform. The fundamental (or first harmonic) frequency has a frequency of f, the second harmonic has a frequency of 2 x f, the third harmonic has a frequency of 3 x f, and the nth harmonic has a frequency of n x f. If the fundamental frequency is 60 Hz (as in the U.S.), the second harmonic frequency is 120 Hz, and the third harmonic frequency is 180 Hz.
The significance of harmonic frequencies can be seen in Fig. 4.3. The second harmonic undergoes two complete cycles during one cycle of the fundamental frequency, and the third harmonic traverses three complete cycles during one cycle of the fundamental frequency.
V1, V2, and V3 are the peak values of the harmonic components that comprise the composite waveform, which also has a frequency of f.
The ability to express a non-sinusoidal waveform as a sum of sinusoidal waves allows us to use the more common mathematical expressions and formulas to solve power system problems. In order to find the effect of a non-sinusoidal voltage or current on a piece of equipment, we only need to determine the effect of the individual harmonics and then vectorially sum the results to derive the net effect. Figure 4.4 illustrates how individual harmonics that are sinusoidal can be added to form a non-sinusoidal waveform.
The Fourier expression in Eq. (4.3) has been simplified to clarify the concept behind harmonic frequency components in a nonlinear periodic function. For the purist, the following more precise expression is offered. For a periodic voltage wave with fundamental frequency of-
ω = 2πf,
v(t) = V0 + ∑(ak cos kωt + bk sin k ωr) (for k- 1 to ∞)…(4.4)
Where ak and bk are the coefficients of the individual harmonic terms or components. Under certain conditions, the cosine or sine terms can vanish, giving us a simpler expression. If the function is an even function, meaning f (-t) = f(t), then the sine terms vanish from the expression. If the function is odd, with f (- t) = – f(t) then the cosine terms disappear.
For our analysis, we will use the simplified expression involving sine terms only. It should be noted that having both sine and cosine terms affects only the displacement angle of the harmonic components and the shape of the nonlinear wave and does not alter the principle behind application of the Fourier series. The coefficients of the harmonic terms of a function-
f(t) contained in Eq. (4.4) are determined by- Coefficient
The coefficients represent the peak values of the individual harmonic frequency terms of the nonlinear periodic function represented by f (t).
Harmonic Number (h):
Harmonic number (h) refers to the individual frequency elements that comprise a composite waveform. For example, h = 3 refers to the third harmonic component with a frequency equal to third times the fundamental frequency. If the fundamental frequency is 60 Hz, then the 3rd (third) harmonic frequency is 3 x 60, or 180 Hz. The harmonic number 6 is a component with a frequency of 360 Hz.
Dealing with harmonic numbers and not with harmonic frequencies is done for two reasons. The fundamental frequency varies among individual countries and applications. The fundamental frequency in the U.S. is 60 Hz, whereas in Europe and many Asian countries it is 50 Hz. Also, some applications use frequencies other than 50 or 60 Hz; for example, 400 Hz is a common frequency in the aerospace industry, while some AC systems for electric traction use 25 Hz as the frequency.
The inverter part of an AC adjustable speed drive can operate at any frequency between zero and its full rated maximum frequency, and the fundamental frequency then becomes the frequency at which the motor is operating. The use of harmonic numbers allows us to simplify how we express harmonics. The second reason for using harmonic numbers is the simplification realized in performing mathematical operations involving harmonics.
Types of Harmonics:
Odd and Even Order Harmonics:
As their names imply, odd harmonics have odd numbers (e.g., 3, 5, 7, 9, 11), and even harmonics have even numbers (e.g., 2, 4, 6, 8, 10). Harmonic number 1 is assigned to the fundamental frequency component of the periodic wave. Harmonic number 0 represents the constant or DC component of the waveform. The DC component is the net difference between the positive and negative halves of one complete waveform cycle.
Figure 4.5 shows a periodic waveform with net DC content. The DC component of a waveform has undesirable effects, particularly on transformers, due to the phenomenon of core saturation. Saturation of the core is caused by operating the core at magnetic field levels above the knee of the magnetization curve. Transformers are designed to operate below the knee portion of the curve.
When DC voltages or currents are applied to the transformer winding, large DC magnetic fields are set up in the transformer core. The sum of the AC and the DC magnetic fields can shift the transformer operation into regions past the knee of the saturation curve. Operation in the saturation region places large excitation power requirements on the power system. The transformer losses are substantially increased, causing excessive temperature rise. Core vibration becomes more pronounced as a result of operation in the saturation region.
We usually look at harmonics as integers, but some applications produce harmonic voltages and currents that are not integers. Electric arc furnaces are examples of loads that generate non-integer harmonics. Arc welders can also generate non-integer harmonics. In both cases, once the arc stabilizes, the non-integer harmonics mostly disappear, leaving only the integer harmonics.
The majority of nonlinear loads produce harmonics that are odd multiples of the fundamental frequency. Certain conditions need to exist for production of even harmonics. Uneven current draw between the positive and negative halves of one cycle of operation can generate even harmonics. The uneven operation may be due to the nature of the application or could indicate problems with the load circuitry. Transformer magnetizing currents contain appreciable levels of even harmonic components and so do arc furnaces during startup. Sub-harmonics have frequencies below the fundamental frequency and are rare in power systems.
When sub-harmonics are present, the underlying cause is resonance between the harmonic currents or voltages with the power system capacitance and inductance. Sub-harmonics may be generated when a system is highly inductive (such as an arc furnace during startup) or if the power system also contains large capacitor banks for power factor correction or filtering. Such conditions produce slow oscillations that are relatively un-damped, resulting in voltage sags and light flicker.
Causes of Voltage and Current Harmonics:
A pure sinusoidal waveform with zero harmonic distortion is a hypothetical quantity and not a practical one. The voltage waveform, even at the point of generation, contains a small amount of distortion due to non-uniformity in the excitation magnetic field and discrete spatial distribution of coils around the generator stator slots. The distortion at the point of generation is usually very low, typically less than 1.0%.
The generated voltage is transmitted many hundreds of miles, transformed to several levels, and ultimately distributed to the power user. The user equipment generates currents that are rich in harmonic frequency components, especially in large commercial or industrial installations. As harmonic currents travel to the power source, the current distortion results in additional voltage distortion due to impedance voltages associated with the various power distribution equipment, such as transmission and distribution lines, transformers, cables, buses, and so on.
Figure 4.9 illustrates how current distortion is transformed into voltage distortion. Not all voltage distortion, however, is due to the flow of distorted current through the power system impedance. For instance, static uninterruptible power source (UPS) systems can generate appreciable voltage distortion due to the nature of their operation. Normal AC voltage is converted to DC and then reconverted to AC in the inverter section of the UPS. Unless waveform shaping circuitry is provided, the voltage waveforms generated in UPS units tend to be distorted.
As nonlinear loads are propagated into the power system, voltage distortions are introduced which become greater moving from the source to the load because of the circuit impedances. Current distortions for the most part are caused by loads. Even loads that are linear will generate nonlinear currents if the supply voltage waveform is significantly distorted.
When several power users share a common power line, the voltage distortion produced by harmonic current injection of one user can affect the other users. This is why standards are being issued that will limit the amount of harmonic currents that individual power users can feed into the source.
The major causes of current distortion are nonlinear loads due to adjustable speed drives, fluorescent lighting, rectifier banks, computer and data-processing loads, arc furnaces, and so on. One can easily visualize an environment where a wide spectrum of harmonic frequencies are generated and transmitted to other loads or other power users, thereby producing undesirable results throughout the system.


Slot Harmonics Definition
Troubleshooting harmonic problems can be like trying to find a needle in a haystack. Every individual load on every branch circuit is a potential harmonic source. However, you can significantly reduce troubleshooting time by determining the harmonic power flow direction on a circuit. Let's say there's a harmonic issue on a branch circuit with ten loads. You would need to connect a monitoring instrument to each load individually, recording the information as you move from load to load. But instruments with a harmonic power flow feature would allow you to conduct the “half way” method of troubleshooting. This means you can connect the instrument after the first five loads to determine if the harmonic is coming from the load or the source. From there, you can connect half way on the initial first five loads and repeat the process.
Most monitoring instruments determine harmonic power flow direction the same way — by comparing the voltage and current waveforms of a harmonic frequency for a particular phase. If the waveforms are inphase ±90 deg, the harmonics come from the source. If they are out-of-phase ±90 deg, they come from the load.
Despite this similarity, monitoring instruments use different methods for compensating for induced phase shifts — if they do at all. In addition, instruments vary widely in how they capture and display data. You'll need to consider these factors to ensure accuracy in determining power flow direction.
Potential Errors
There are a number of items that can cause inaccurate harmonic direction, including current-transformer (CT) and potential-transformer (PT) phase shifts, calibration, sampling, and frequency response. Because direction is based on the phase relationship between voltage and current, any phase shift causes a degree of uncertainty that correlates with a potential error.
Table 1 shows the specifications for a typical clamp-on transformer. Note that the phase shift changes as the load changes. Table 2, on page 36, shows how the accuracy changes as the frequency changes. This could adversely affect the harmonic direction indication by reducing the level of amplitude on the current.
Slot Harmonics Define Government
In Fig. 1, on page 36, you'll see typical response curves from current transducers. As the frequency increases, the phase shift also increases. Therefore, if a current transformer has a ±3 deg phase shift, the degree of uncertainty (or the chance of coming up with incorrect power flow direction) would be 12 ÷ 360 × 100 or 3.33%. The reasoning is as follows: Because direction changes from the source to the load (or vice versa) at 90 deg and 270 deg and the transformer error is ± 3 deg, there is a degree of uncertainty between 87 deg and 93 deg and 267 deg and 273 deg.
This error also can occur if you use an instrument that employs internal PTs, if you connect an instrument to external PTs, or if you clip a CT around the secondary of another CT. (Caution: These errors are additive. If you connect the instrument to all of these transformers, the error can be substantial.)
Sources of other potential errors include the following:
- The harmonic magnitude of the voltage and/or current waveform is low. In this case, the circuitry may not be able to accurately distinguish the phase angle, thus hampering the accuracy of the harmonic direction.
- A CT pointing the wrong way or voltage leads connected incorrectly cause inaccurate directional indications. Many manufacturers allow users to view phasor diagrams, which show the phase rotation between phases. This helps ensure that the voltage and current leads are connected properly. Negative power or power factor can be indicative of a CT pointing the wrong way or improperly connected voltage leads.
To help minimize any errors that may arise, it's best to select a quality current transducer with a low phase shift and a good frequency response.
Fortunately, some manufacturers have gotten into the act by enhancing their products with features also designed to minimize errors. At some facilities, instruments are calibrated for phase shift by matching current transducers to the CTs being used. This eliminates CT errors — as long as the CTs are not interchanged.
Yet another instrument provides a calibration probe that calibrates current transducers in the field. This permits users to switch CTs and still get accurate readings. It also compensates for any frequency response errors. The challenge here is similar to the one for CTs. That is, the accuracy of the probes must be recognized or additional error will be introduced.
Power Flow Presentation
Most instruments that determine harmonic power flow direction display the resulting information in waveform captures or snapshots. For example, some instruments display the harmonic magnitude and cosine of the phase angle (or power factor). Because the power factor's sign is indicative of direction, the user can determine if harmonic power flow comes from the source or from the load.
Other instruments display the angle of the harmonic and voltage waveform. This allows the user to interpret the direction visually from the angle. If the angle is to the right of the y-axis, the harmonic stems from the source; if it's on the left, it comes from the load.
Still other instruments display a directional bar graph that shows a harmonic spectrum. If the harmonic appears above the x-axis, it comes from the source. If it appears below the x-axis, it originates from the load.
The problem with relying on waveform captures or snapshots is the possibility of inaccurate assumptions. Because the information is recorded at intervals, any change in the harmonic information between the snapshots is not recorded and missed forever.
Fortunately, there are instruments available that can display graphs of harmonic magnitudes and phases over time. This type of display captures harmonic data between snapshots, providing a cycle-by-cycle resolution of the harmonic (see Fig. 2, on page 36). The phase graph indicates whether harmonic direction comes from the load or from the source.
Some instruments have no display area and require a computer to view information. Others have graphical or alphanumeric displays for viewing real-time bar graphs and values.
Slot Harmonics Define Math
In many cases, instruments with built-in displays cost significantly more than those with no displays, and they can sometimes compromise the weatherproof rating of the case. Memory slots and push buttons can leak and cause damage to the monitoring equipment.
Some engineers use optional hand-held devices to download real-time data. This eliminates the need for a graphical display and typically lowers the cost of the base unit. The user can then download and view the information in a controlled environment.
Instruments that indicate harmonic power flow direction are beneficial for troubleshooting harmonic problems. However, engineers should watch for errors that could adversely affect direction accuracy. These errors include incorrect hookups, low voltage or current, the frequency response of current transducers, and the phase shift of potential and current transformers.
To minimize these errors, some manufacturers have added enhanced features such as phasor diagrams, probe calibration coils, and factory calibration of current transducers. Whatever instrument you decide to use, you'll have the added advantage of understanding how it gathers and displays information.
Lou Barker is a sales manager for Power Monitors Inc. in Harrisonburg, Va. You can reach him atlbarker@powermonitors.com.